GAUGE REPEATABILITY REPRODUCIBILITY – ĐÁNH GIÁ ĐỘ TIN CẬY CỦA HỆ THỐNG ĐO LƯỜNG – Gauge R&R

1. Khái quát phương pháp Gage R & R
Gauge Repeatability & Reproducibility (GR&R) – Đánh Giá Độ Tin Cậy của Hệ Thống Đo Lường, Một công cụ thống kê đo lường mức dao động hay sai sót trong hệ thống đo lường gây ra bởi thiết bị đo lường hay người thực hiện công tác đo lường.
- Gage: Dụng cụ, thiết bị sử dụng để thực hiện phép đo. Ví dụ: thước kẹp, cân điện tử, ..
- Repeatability – Độ lập lại độ lệch khi đo cùng dụng cụ đo, cùng người đo tiến hành đo nhiều lần. Ví du: cùng một mẫu sản phẩm, một nhân viên QC tiến hành đo mẫu đó n lần bằng thước kẹp hiển thị số (điện tử) thì chúng ta có n kết quả, các kết quả đo này có thể giống nhau và khác nhau, từ kết quả thống kê theo phương pháp Repeatability chúng ta có thể khẳng định được thước kẹp này có sử dụng được hay không với khản sai số cho phép của khoản đo.
- Reproducability – Độ tái lập: độ lệch khi những người đo khác nhau thực hiện đo linh kiện trên cùng dụng cụ đo. Ví dụ: trong phòng QC bạn có 3 người sử dụng chung một thiết bị đo, làm thế nào để bạn chứng minh rằng 3 người này có kết quả đo đủ tin cậy như nhau, công cụ này sẽ giúp bạn biết được điều đó.
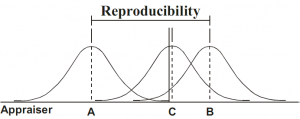
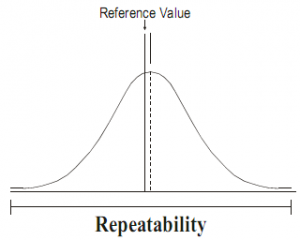
Các nhà sản xuất đang liên tục phấn đấu để cải tiến chất lượng sản phẩm, quy trình sản xuất và giảm một phần sự biến đổi trong quy trình của họ. Trong thực tế luôn có sự biến đổi (biến thiên) tồn tại trong mọi quy trình sản xuất. Hầu hết chúng ta sử dụng các công cụ thống kê SPC để kiểm soát chất lượng sản phẩm, tuy nhiên sự thành công của hệ thống SPC nào phụ thuộc vào sự chính xác của dữ liệu thu được từ quá trình đo. Thật không may, tất cả các dữ liệu đo lường chứa một tỷ lệ phần trăm các độ rung (độ biến đổi, biến thiên) nhất định. Độ rung là sự khác biệt giữa các giá trị thực và các giá trị quan sát được. Các biến đổi đại diện cho số lượng lỗi đo lường. Ngoài những lỗi do đo lường, còn lại là các biến đổi thực tế của sản phẩm hoặc quá trình. Để đảm bảo rằng dữ liệu đo lường của chúng ta là chính xác, chúng ta phải xác định xem lượng biến thiên có được chấp nhận hay không. Một công cụ hiệu quả để đánh giá sự thay đổi của phép đo là Độ lặp lại và Độ lặp lại của Gage (Gage R & R). Như vậy Tổng số các biến đổi chung của quá trình gồm 3 thành phần:
• Các biến đổi sản phẩm/quá trình thực sự (máy thiết bị hao mòn, ….).
• Các biến đổi do thiết bị đo (độ lặp lại – Repeatability: thiết bị đo không ổn định, …).
• Biến đổi do các người vận hành khác nhau (độ tái lập – Reproducability – năng lực của những người khách nhau).
Để đánh giá một phương pháp đo lường của bạn có hiệu quả hay không người ta dùng phương pháp này. Thông thường bạn dùng thước kẹp, các máy đo kích thước, các máy đo cho ra các chi số khác, … để đảm bảo rằng thiết bị và con người vận hành cho ra một kết quả đo có độ tin cậy nhất định thì trước khi thực hiện bạn phải đánh giá trước xem liệu phương pháp đó có cho kết quả ổn định và chính xác không?
Định kỳ chúng ta cũng nên kiểm tra lại thử xem trong quá trình có những biến đổi có ảnh hưởng đến kết quả đo hay không? điều này chứng minh rằng các phương pháp đo và quá trình đo cho dữ liệu tin cậy.
2. THỰC HIỆN
- Chọn N mẫu đo (Đối với việc đánh giá kiểm soát quá trình đo thì N ≥ 10 mẫu, đối với ước lượng sai số máy đo đã ổn định thì lấy N ≥ 30), không nên lấy n mẫu liên tiếp từ dây chuyển sản xuất, mà lấy 10 mẫu cách quản một thời gian nhất định để đảm bảo tính chọn mẫu và đánh giá độ rung từng thời điểm mà không phải một thời điểm.
- Một điểm lưu ý là khi chọn 10 mẫu, bạn nên chọn 3 mẫu gần giới hạn dưới, 4 mẫu gần giữa và 3 mẫu gần giới hạn trên để đảm bảo đủ khoản rộng của mẫu. nếu cho gần quán tâm thì khoản rộng không đủ dẫn đến một số chị số không đạt.
- Đánh dấu các mẫu ngẫu nhiên từ 1 đến N sao cho việc đánh dấu không làm biến đổi kết quả đo.
- Chọn máy đo muốn thực hiện khảo sát (máy đo này phải hoạt động tốt), hiệu chuẩn máy về giá trị đúng;
- Chọn 3 người để thực hiện thao tác đo;
- Tiến hành đo, mỗi người thực hiện lập lại 3 lần trên cùng 1 mẫu đo và cùng 1 thiết bị đo
|
Số mẫu |
Nhân viên A |
Nhân viên B |
Nhân viên C
|
|||||||||
|
Lần 1 |
Lần 2 |
Lần 3 |
Độ lệch Ra |
Lần 1 |
Lần 2 |
Lần 3 |
Độ lệch Rb |
Lần 1 |
Lần 2 |
Lần 3 |
Độ lệch Rc |
|
|
1 |
a11 |
a21 |
a31 |
|
b11 |
b21 |
b31 |
|
c11 |
c21 |
c31 |
|
|
2 |
a12 |
a22 |
a32 |
|
b12 |
b22 |
b32 |
|
c12 |
c22 |
c32 |
|
|
3… |
— |
— |
— |
|
— |
— |
— |
|
— |
— |
— |
|
|
N |
a1n |
a2n |
a3n |
|
b1n |
b2n |
b3n |
|
c1n |
c2n |
c3n |
|
|
X̅ |
X̅a1 |
X̅ a2 |
X̅ a3 |
|
X̅ b1 |
X̅ b2 |
X̅ b3 |
|
X̅ c1 |
X̅ c2 |
X̅ c3 |
|
2.1. Tính Prepeatability
- Độ lập lại EV (equipment Variation) biểu thị sự biến thiên do thiết bị tạo ra.
- Ra1 = Max(a11,a21, a31) – Min((a11,a21, a31); (lấy số lớn nhất – số nhỏ nhất = độ lệch)
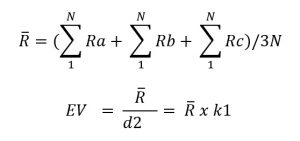
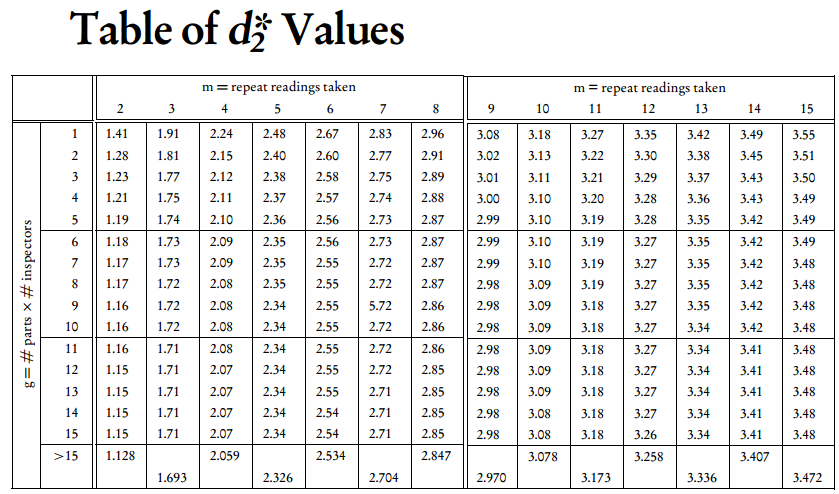
Với d2 được tính theo bản dưới đây, với m là số lần lặp lại, g số nhóm con (g = số người đo x số mẫu đo).
2.2. Tính reproducibility:
Độ tái lập AV (appraiser variation) biểu thị sự biến thiên do người đo tạo ra.
Để tính toán độ tái lập, còn được gọi là độ biến thiên của trình thẩm định (AV), sử dụng công thức sau:
AV = √ (( Xdiff * k 2 ) 2 – (EV) 2 / (n * r))
Với:
- AV = độ tái lập
- X̅ DIFF = [Max X̅appraiser] – [Min X̅appraiser] : phạm vi trung bình của người vận hành
- EV = độ lặp lại
- k 2 = Tra bảng
- n = số mẫu đo
- r = số lượng thử nghiệm trên mỗi mẫu (số lần lập lại).
Tìm k 2 :
- Để tìm giá trị k2 để sử dụng trong việc tìm d2 . Để làm điều này, bạn sẽ cần m và g một lần nữa. Nhưng chúng ta sẽ sử dụng một con số khác nhau cho m .
- m là kích thước nhóm con. Khi tìm k2 , đây là số lượng người đo (operator).
- g là số nhóm con = số lượng mẫu x số người đo.
2.3. Tính toán R & R của Gage
Không có gì đáng ngạc nhiên, Gage R & R được tính bằng cách kết hợp các số liệu độ lặp lại và độ lặp lại, sử dụng công thức này:
Gage R & R = √ (EV2 + AV2 )
Với:
- AV = độ tái lập
- EV = độ lặp lại
Nếu tính toán ta thấy rằng AV lớn hơn EV thì sai số do người đo lớn hơn thiết bị đo, chúng ta tiến hành cải tiến thao tác người đo và đánh giá lại năng lực người đo;
Nếu tính toán cho thấy AV < EV thì sai số do thiết bị tạo ra lớn hơn sai số do người đo, ta tiến hành cải tiến thiết bị đo.
2.4. Tính PV, TV và ndc
PV, TV và GRR được phân biệt theo hình như sau:
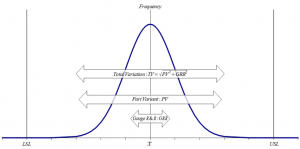
PV (Part Variation) = Rp x K3, với
- Rp = (Max X̅part – Min X̅part);
- K3 hệ số tra theo bảng sau:
|
Part |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
K3 |
0.7071 |
0.5231 |
0.4467 |
0.403 |
0.3742 |
0.3534 |
0.338 |
0.325 |
0.3136 |
- TV (Total Variation) = √ (GRR 2 + PV 2)
- ndc = √2(PV/GRR) = 1.41 (PV/GRR).
Dấy bình phương của GRR và PV nói lên không lấy giá trị âm, vì lấy giá trị âm thì đôi khi TV âm vô nghĩa.
ndc là số loại giá trị đo có thể được phân biệt một cách đáng tin cậy. Nói một cách đơn giản, bạn có thể đếm số lần GRR độ lặp lại và độ tái lập của máy đo phù hợp với biến quá trình thực tế.
- ndc ≥ 5 đạt, ndc < 5 chưa đạt. Số 5 biểu thị cho việc khảo sát phải bao phủ cả 5 vùng của hình chung khảo sát như hình bên dưới.
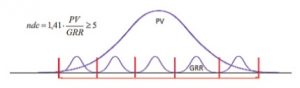
Bạn luôn rút gọn số của ndc, trừ khi nó nhỏ hơn 1. Nếu nó nhỏ hơn 1, bạn phải làm tròn nó lên. Hệ số 1,41 (= √2) không liên quan đến khoảng tin cậy 97%. Nó được tính toán từ các tỷ lệ biến thiên được đưa ra trong biểu đồ ISO.
Hướng dẫn sử dụng MSA cho biết ndc phải lớn hơn hoặc bằng 5. Ý nghĩ đằng sau đặc điểm kỹ thuật này là việc kiểm soát quy trình chỉ có ý nghĩa trong trường hợp bạn có thể chia quy trình thành ít nhất 5 loại giá trị đo lường khác nhau dựa trên ndc (xem hình). Nghĩa là hệ thống đo lường phải tách biệt được sai số của dụng cụ đo và dao động của vật đo theo 5 hình chung nhỏ GRR.
2.4. Kết luận
- Gage R&R/TV dưới 10% = ACCEPTABLE – Chấp nhận– Không yêu cầu hành động (10%: có nghĩa là tổng sai số do con người và thiết bị phải nhỏ hơn 10%).
- Từ 10% đến 30% = MARGINAL– Có thể chấp nhận: Nếu Ppk nhỏ hơn 1,67, thì hãy cải tiến quá trình đo cho đến khi % dung sai nhỏ hơn 10%, nếu Ppk lớn, không cần thực hiện hành động nào.
- Lớn hơn 30% = UNACCEPTABLE– Không chấp nhận: Phải cải tiến quy trình đo lường để % dung sai nhỏ hơn 10% hoặc dưới 30% với Ppk lớn hơn 1,67.
- ndc ≥ 5 đạt, ndc < 5 chưa đạt.
Tuy nhiên xét về sự tương quan giữa %GRR và ndc ta có biểu thức sau:
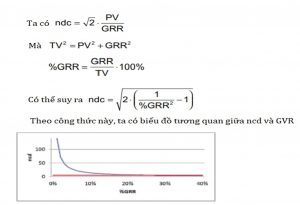
Vì vậy, ndc là 14 trong trường hợp %GRR = 10% và ndc là 4 khi% GRR = 30%. Rất tiếc, giới hạn ndc = 5 được tìm thấy cho% GRR = 27,2% không khớp với giới hạn cho% GRR < 10%.
3. Ví dụ thực tế:
3.1. Variable Gage Repeatability & Reproducibility – Độ biến đổi (độ rung)
Chọn 3 người thực hiện đo 3 mẫu sản phẩm, lập lại 4 lần.
Khi bạn đã hoàn thành bản ghi đo lường của mình, kết quả của bạn sẽ giống như thế này:
3.1. Variable Gage Repeatability & Reproducibility – Đo mẫu
Chọn 3 người thực hiện đo 10 mẫu sản phẩm, lập lại 3 lần, ta có kết quả như sau
Khi bạn đã hoàn thành bản ghi đo lường của mình, kết quả của bạn sẽ giống như thế này:
|
Người đo |
Số lần lập lại |
Lượng mẫu (Part) |
Trung bình |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
A |
1 |
0.29 |
-0.56 |
1.34 |
0.47 |
-0.80 |
0.02 |
0.59 |
-0.31 |
2.26 |
-1.36 |
0.194 |
|
2 |
0.41 |
-0.68 |
1.17 |
0.50 |
-0.92 |
– 0.11 |
0.75 |
0.20 |
1.99 |
-1.25 |
0.166 |
|
|
3 |
0.64 |
-0.58 |
1.27 |
0.64 |
-0.84 |
-0.21 |
0.66 |
-0.17 |
2.01 |
-1.31 |
0.211 |
|
|
Trung bình X̅aj =(X1+X2+X3)/3 |
0.447 |
-0.607 |
1.260 |
0.537 |
-0.853 |
-0.100 |
0.667 |
-0.227 |
2.087 |
-1.307 |
X̅a = ƩX̅aj/n = 0.1903 |
|
|
Khoản Raj = Xmax – Xmin |
0.35 |
0.12 |
0.17 |
0.17 |
0.12 |
0.23 |
0.16 |
0.14 |
0.27 |
0.11 |
Ṝa = Ʃ Raj /n = 0.184 |
|
|
B |
1 |
0.08 |
-0.47 |
1.19 |
0.01 |
-0.56 |
-0.20 |
0.47 |
-0.63 |
1.80 |
-1.68 |
0.001 |
|
2 |
0.25 |
-1.22 |
0.94 |
1.03 |
-1.20 |
0.22 |
0.55 |
0.08 |
2.12 |
-1.62 |
0.115 |
|
|
3 |
0.07 |
-0.68 |
1.34 |
0.20 |
-1.28 |
0.06 |
0.83 |
-0.34 |
2.19 |
-1.50 |
0.089 |
|
|
Trung bình X̅bj =(X1+X2+X3)/3 |
0.133 |
-0.790 |
1.157 |
0.413 |
-1.013 |
0.027 |
0.617 |
-0.297 |
2.037 |
-1.60 |
X̅b = ƩX̅bj/n = 0.0683 |
|
|
Khoản Rbj = Xmax – Xmin |
0.18 |
0.75 |
0.40 |
1.02 |
0.72 |
0.42 |
0.36 |
0.71 |
0.39 |
0.18 |
Ṝb = Ʃ Rbj /n = 0.513 |
|
|
C |
1 |
0.04 |
-1.38 |
0.88 |
0.14 |
-1.46 |
-0.29 |
0.02 |
-0.46 |
1.77 |
1.49 |
-0.223 |
|
2 |
-0.11 |
-1.13 |
1.09 |
0.20 |
-1.07 |
-0.67 |
0.01 |
-0.56 |
1.45 |
-1.77 |
-0.256 |
|
|
3 |
-0.15 |
-0.96 |
0.67 |
0.11 |
-1.45 |
-0.49 |
0.21 |
-0.49 |
1.87 |
-2.16 |
-0.284 |
|
|
Trung bình X̅cj =(X1+X2+X3)/3 |
-0.073 |
-1.157 |
0.880 |
0.150 |
-1.327 |
-0.483 |
0.080 |
-0.503 |
1.697 |
-1.807 |
X̅c = ƩX̅cj/n = -0.2543 |
|
|
Khoản Rcj = Xmax – Xmin |
0.19 |
0.42 |
0.42 |
0.09 |
0.39 |
0.38 |
0.20 |
0.10 |
0.42 |
0.67 |
Ṝc = Ʃ Rcj /n = 0.328 |
|
3.1.1. Tính trung bình từng mẫu của 3 người đo
với i là số người đo i = A, B, C;
j: là số lượng mẫu, j = 1,2,3…. 10
X̅i1 = ƩX̅i1/i = (X̅a1 + X̅b1 + X̅c1 )/ 3 ={ 0.447 + 0.133 + (-0.073 )}/ 3 = 0.169, tương tự ta có bản sau:
|
Người đo |
Số lần lập lại |
Lượng mẫu (Part) |
Trung bình |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
Trung bình X̅ij |
0.169 |
-0.851 |
1.099 |
0.367 |
-1.064 |
-0.186 |
0.454 |
-0.342 |
1.940 |
-1.571 |
= ƩX̅ij/n = 0.0014 |
|
3.1.2. Tính Khoản đo cho mỗi người đo
Tính X̅ DIFF = [Max X̅ = X̅a = 0.1903] – [Min X̅ = X̅c = -0.2543] = 0.4446
3.1.3. Tính ![]()
![]() = ([Ṝa = 0.184] + [Ṝb = 0.513] + [Ṝc = 0.328]) / [ Số người đo = 3] = 0.3417
= ([Ṝa = 0.184] + [Ṝb = 0.513] + [Ṝc = 0.328]) / [ Số người đo = 3] = 0.3417
3.1.4. Tính Rp
Rp = X̅ij max – X̅ijmin = [X̅9 = 1.940] – [X̅10 = – 1.571] = 3.511
3.1.5. Tìm k 1
Thông thường Số lần lập lại = 3, thì k1 = 0.5908, Số lần lập lại = 2, thì k1 = 0.8862
Cách tính k1 như sau:
Tra cứu bảng d2 để tìm giá trị d 2 để sử dụng trong việc tìm k 1 . Để làm điều này, bạn sẽ cần hai biến:
m là kích thước nhóm con. Khi tìm k1 , đây là số lần mà mỗi phép đo được lặp lại. Vậy m = 3.
g là số nhóm con. Đây là số lượng kết hợp của số mẫu và người đo. Trong dữ liệu thử nghiệm chúng ta đang sử dụng, có 3 vận hành(A,B,C) và 10 mẫu (1…10). Vậy g = 3 x 10 = 30.
Tra bản d2 với m = 3 và g = 30 thì d2 = 1.693
- d2 = 1.693
- k1 = 1 / d2
- k1 = 1 / 1.693
- k1 = 0.5908
4. Tính toán độ lặp lại
Để tính toán độ lặp lại, còn được gọi là phương sai thiết bị (EV), sử dụng công thức sau:
- EV = * (k1 )
- EV = 0.3417 x 0.5908
- EV = 0.20188
5. Tìm k 2
Đối với 2 người đo, lập lại 3 lần và 10 mẫu thì K2 = 0.7071. Đối với 3 người đo, lập lại 3 lần và 10 mẫu thì K2 is 0.5231
6. Tính toán độ tái lập
Để tính toán độ tái lập, còn được gọi là độ biến thiên của trình thẩm định (AV), sử dụng công thức sau:
AV = √ (( X diff * k 2 ) 2 – (EV) 2 / (n * r))
Trong đó:
- AV = độ tái lập
- X diff = phạm vi trung bình của người đo
- EV = độ lặp lại
- k 2 = 0.5231
- n = số lượng mẫu (1…10) = 10
- r = số lần lập lại = 3 lần
AV = √ ((X diff * k 2 ) 2 – (EV) 2 / (n * r))
AV = √ ((0.4446 x 0.5) 2 – (0.20188) 2 / (10 * 3))
AV = 0.22963
Trong trường hợp AV âm thì hãy lấy AV = 0.
7. Tính toán R & R của Gage
Không có gì đáng ngạc nhiên, Gage R & R được tính bằng cách kết hợp các số liệu độ lặp lại và độ lặp lại, sử dụng công thức này:
Gage R & R = √ (EV 2 + AV 2 )
Ở đâu:
- AV = độ tái lập
- EV = độ lặp lại
Vì vậy, sử dụng dữ liệu của chúng ta từ phía trên:
Gage R & R = √ (EV 2 + AV 2 )
Gage R & R = √ ((0.20188)2 + 0.22963 2 )
Gage R & R = 0,30575
- Tính độ Biến động do sản phẩm PV (Part Variation).
Ta có: PV = Rp x K3
với Rp = ẌPartmax – ẌPartmax (Số trung bình lớn nhất – Số trung bình nhỏ nhất)
Rp = 3.511
K3 tính theo bảng sau:
|
Parts (phần tử) |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
K3 |
0.7071 |
0.5231 |
0.4467 |
0.4030 |
0.3742 |
0.3534 |
0.3375 |
0.3249 |
0.3146 |
PV = Rp x K3 = 3.511 x 0.3146 (n = 10 mẫu) = 1.10456
- Tính TV, %GRR, %PV
- TV = √ (GRR 2 + PV 2) = √(0.30575 2 + 1.10456 2 ) = 1.14610
- %GRR/TV = 100 [0.30575/1.14610]= 26.68%
- % PV = 100 [PV/TV] = 100 [1.10456/1.14610] = 96.38%
- ncd = 1.41 (PV/GRR) = 1.41(1.10456/0.30575) = 5.094 ~ 5
–> Vậy %GRR = 26.68 %, nằm trong khoản 10% < %GRR < 30%, để biết tiến hành cải tiến không ta phải tính chỉ số Ppk, nếu Ppk nhỏ hơn 1,67 thì xem xét EV hay AV cái nào cao hơn thì tập trung cải tiến chỉ số đó, còn Ppk > 1,67 thì không nhất thiết cải tiến.
–> ndc =5.094 > 5 : Chấp nhận hệ thống đo lường
———————————
Nguyễn Hoàng Em
Tài liệu tham khảo:
https://quality-one.com/grr/
https://fr.wikipedia.org/wiki/Gage_R%26R
https://sixsigmastudyguide.com/repeatability-and-reproducibility-rr/
https://hainguyendt.wordpress.com/2018/11/19/bien-dong-trong-he-thong-do-luong-phan-4-gage-rr/
https://www.isixsigma.com/tools-templates/measurement-systems-analysis-msa-gage-rr/making-sense-attribute-gage-rr-calculations/
https://www.q-das.com/fileadmin/mediamanager/PIQ-Artikel/Crux_ndc.pdf
MEASUREMENT SYSTEMS ANALYSIS – Reference Manual, Fourth Edition, copyright 2010, ISBN#: 978-1-60-534211-5









Mình thấy k1,k2, k3 có nhiều nơi họ không lấy 1/d2 mà lấy 5.15/d2, có nơi lấy 6/d2, bạn có thể giải thích thêm tại sao được không ?
Và, 3 người đo, 10 mẫu, mỗi mẫu đo 10 lần thì k2,k3 họ lấy giá trị g=1 để tra bảng tìm d2, cũng không hiểu vì sao luôn ?